A New Way to Play rock, scissor, papers

Background

Have you ever played the game "rock, scissor, pepers"? That's a funny game, and it's fair on the premise that no one cheated.

Problem

Just imagine this scenario: There is a essential gambling between A and B. And the "rock, scissor, papers" is the most important part of the gambling, A and B are both notorious for their expertise in cheating. To make sure that the gambling is fair, you must thought out of a way which is easy to understand and realize.

The first step to stop cheating is to understand how to cheat. So, how will the cheater do? If I want to cheat, I will not show my decition until my enemy show his decition. What I show is based on what the enemy show so I will win. However, if the enemy uses the same trick, the game won't end.

So, the game won't be fair until the problem that each side can't show their decition the same time, which is very hard to solve. What's your idea about this problem?

First solvtion

The first solvtion is to force each other to tell their decition to the the third person, who is reliable enough and he won't tell anyone the other's dicition and he won't accept bribes and revise the other's decition surreptitiously.

But there is a obvious loophole: How to make sure that the third person is reliable? This gambling is really important to each side, and you know A and B well, they are very good at cheating so it's quite possible that they will do everything they can to make the third person do as they will. Remember, no one in the world is always reliable, so the approach is hard to practice.

Second solvtion

There are nothing always reliable except math. In order for you to understand this approach, we have to introduce a new concept named "hash".

What's hash?

Hash is a concept in cryptographic programming. To simplifiy this conception, you can take it as a function that has one input and one output, which it is quite easy to get the output from the input and almost impossible to get the input from the output by using it. What's more, one output only correspond to one input, which means that if b = hash(a), b = hash(c), then a equals to c.

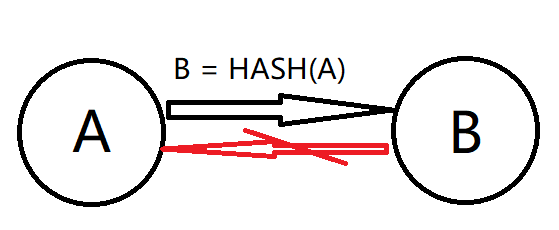
How to take the advantage of the special properity of hashing?

1. both side thought out of a random num, and keep the num as a secret.
2. both side calculate the hash of their num.
3. both side provide their hash to the other, the sequence is not importent.
4. after both side's hash are provided, both side show their own num.
5. both side check whether or not the other had cheated by using the hash algorighm to calc the num of the other's hash, the hash algorithm is open to each other so that it's not difficult. if the hash equals to the hash the other provide before, the other is honest.

Which is better?

The first solution is the traditional solution to most of problems about truth: To find a man or institution which each sides trust, such as bank. The second solution is a super cool solution to these kinds of problems: By some means of cryptographic, which the blockchain uses and have got a great success by. Have you ever played the game "rock, scissor, pepers"? That's a funny game, and it's fair on the premise that no one cheated.